# -*- coding: utf-8 -*-
 # author: 'boliang'
 # date: 2018/4/15 23:39
 
 import math
 import matplotlib.pyplot as plt
 import numpy as np
 
 class Solution_qmin(object):
     def __init__(self, fun=None, epslion=1e-5, deta=1e-4, a=0, b=0, alpha=0, h0=0.5):
         if fun == None:
             return
         self.reset(fun, epslion, deta, a, b, alpha, h0)
 
    def reset(self, fun, epslion=1e-5, deta=1e-4, a=0, b=0, alpha=0, h0=0.5):
         self.__fun = lambda x: eval(fun)
        self.__fun_str = fun
         self.__epslion = epslion
         self.__deta = deta
         if a == 0 and b == 0:
             self.__a, self.__b = self.__get_section(alpha, h0)
        else:
             self.__a = a
             self.__b = b
 
     # 进退法, 获得极小值点的搜索区间
     def __get_section(self, alpha, h):
         ak = alpha
         k = 0
         cal_k = self.__fun(ak)
        while True:
             akp = ak + h
             cal_kp = self.__fun(akp)
            if cal_kp < cal_k:
                 h = 2*h
                 alpha = ak
                ak = akp
                cal_k = cal_kp
                k += 1
             else:
                 if k == 0:
                     # 反向搜索
                     h = -h
                     alpha = akp
                    akp = ak
                    cal_kp = cal_k
                    k = 1
                 else:
                     break
 
 
         return [min(alpha, akp), max(alpha, akp)]
 
    def __draw_image(self, min_x, min_y):
         X = np.arange(self.__a-5, self.__b+5, 0.01)
        Y = list(map(lambda x: self.__fun(x), X))
        plt.plot(X, Y)
        plt.title(self.__fun_str, fontSize=16)
        plt.xlabel('X', fontSize=16)
        plt.ylabel('Y', fontSize=16)
        plt.text(min_x, min_y, 'X', color='red', fontSize=14)
        plt.text(min_x+0.382, min_y-0.618, '({:.4f}, {:.4f})'.format(min_x, min_y), fontSize=14)
        plt.show()
 
    # 抛物线法搜索极小值点
     def run(self):
         step = 1
         h = (self.__b - self.__a)/2
         s0 = self.__a
        s1 = s0 + h
        s2 = s0 + 2*h
        cal_0 = self.__fun(s0)
        cal_1 = self.__fun(s1)
        cal_2 = self.__fun(s2)
 
        while abs(s2 - s0) >= self.__epslion and abs(h) > self.__deta and step < 20:
             #更新步长h, 计算插值点
             d = (2*(2*cal_1 - cal_0 - cal_2))
            pre_h = h
            h = (4*cal_1 - 3*cal_0 - cal_2)*h / d
 
            if abs(h - pre_h) < self.__epslion:
                 break
 
             s_tmp = s0 + h
            cal_tmp = self.__fun(s_tmp)
 
            # 插值点函数计算值比中间点要大
             if cal_1 <= cal_tmp:
 
                 # 插值点在右半峰上, 更新右边区间端点
                 if s1 < s_tmp:
                     s2 = s_tmp
                    cal_2 = cal_tmp
 
                # 插值点在右半峰，更新左边区间端点
                 else:
                     s0 = s_tmp
                    cal_0 = cal_tmp
 
            # 插值点函数计算值比中间点要小
             else:
                 # 插值点在右半峰，更新右端点
                 if s1 > s_tmp:
                     s2 = s1
                    cal_2 = cal_1
                # 插值点在左半峰，更新左端点
                 else:
                     s0 = s1
                    cal_0 = cal_1
 
                # 更新中间点
                 s1 = s_tmp
                cal_1 = cal_tmp
            step += 1
 
         result = {
            '极小值点为：': s1,
             '极小值为：': cal_1,
             '迭代次数为：': step,
             '|s2-s0|：': abs(s2 - s0),
             '|fun(s2)-fun(s0)|：': abs(cal_2 - cal_0)
        }
 
        for key, value in result.items():
             print(key, value)
 
        self.__draw_image(s1, cal_1)
 
 if __name__ == '__main__':
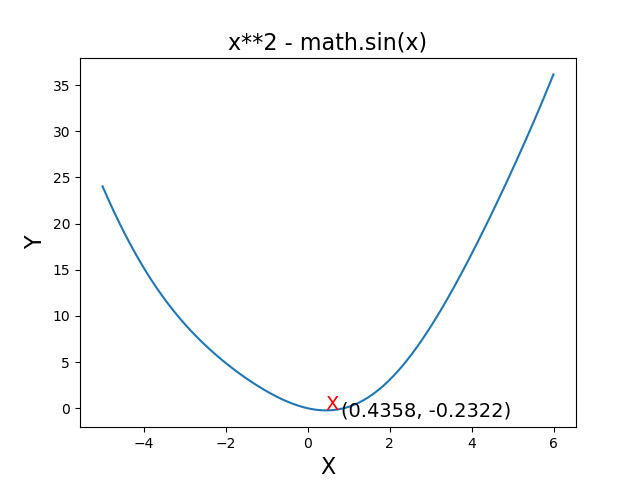
     Solution_qmin('x**2 - math.sin(x)', 1e-5, 1e-4, 0, 1).run()