实现代码如下
# -*- coding: utf-8 -*-
# author: 'boliang'
# date: 2018/3/13 8:46
import random
import numpy as np
import matplotlib.pyplot as plt
class Solution(object):
best_eval = 0
def __init__(self, level=30, mating_rate=0.88, mutate_rate = 0.1, cal_level=1000):
self.mating_rate = mating_rate
self.mutate_rate = mutate_rate
self.cal_level = cal_level
self.level = level
self.C = []
self.min_index = -1
self.cities = [
[1304, 2312],
[3639, 1315],
[4177, 2244],
[3712, 1399],
[3488, 1535],
[3326, 1556],
[3238, 1229],
[4196, 1004],
[4312, 790],
[4386, 570],
[3007, 1970],
[2562, 1756],
[2788, 1491],
[2381, 1676],
[1332, 695],
[3715, 1678],
[3918, 2179],
[4061, 2370],
[3780, 2212],
[3676, 2578],
[4029, 2838],
[4263, 2931],
[3429, 1908],
[3507, 2367],
[3394, 2643],
[3439, 3201],
[2935, 3240],
[3140, 3550],
[2545, 2357],
[2778, 2826],
[2370, 2975]
]
self.x_len = len(self.cities)
for i in range(level):
tmp = list(self.cities)
random.shuffle(tmp)
self.C.append(tmp)
#评估函数
def __Eval__(self, C):
dis = 0
length = len(C)
city_1 = C[0]
for i in range(1, length):
city_2 = C[i]
dis += np.sqrt((city_1[0]-city_2[0])**2 + (city_1[1]-city_2[1])**2)
city_1 = city_2
city_1 = C[0]
city_2 = C[length-1]
dis += np.sqrt((city_1[0]-city_2[0])**2 + (city_1[1]-city_2[1])**2)
return dis
#计算最小适应值
def __get_best__(self):
cal_eval = list(map(lambda C:self.__Eval__(C), self.C))
length = len(cal_eval)
for i in range(length):
if self.min_index == -1 or cal_eval[i] < cal_eval[self.min_index]:
self.min_index = i
return cal_eval[self.min_index]
#选择
def __select__(self):
C_evals = list(map(lambda C:self.__Eval__(C), self.C))
eval_sum = sum(C_evals)
tmp_evals = list(map(lambda eval:eval_sum/eval, C_evals))
eval_sum = sum(tmp_evals)
tmp_rates = list(map(lambda eval:eval/eval_sum, tmp_evals))
C_rates = list(map(lambda index:sum(tmp_rates[:index+1]), range(self.level)))
tmp_C = []
while len(tmp_C) < self.level:
num = random.random()
tmp = list(C_rates)
tmp.reverse()
for rate in tmp:
if num >= rate:
tmp_C.append(self.C[C_rates.index(rate)])
break
self.C = tmp_C
#交配
def __mating__(self):
select_mating_indexs = [cor for cor in range(self.level) if random.random() < self.mating_rate]
for i in select_mating_indexs:
mating_bit = random.randint(0, self.x_len - 1)
tmp = []
for t in self.C[i][mating_bit:]:
tmp.append(list(t))
random.shuffle(tmp)
self.C[i][mating_bit:] = tmp
#变异
def __mutate__(self):
for coord in range(self.level):
mutate_indexs = [cor for cor in range(self.x_len) if random.random() < self.mutate_rate]
length = len(mutate_indexs)
if length & 1 == 0:
random.shuffle(mutate_indexs)
for index in range(0, length, 2):
self.C[coord][mutate_indexs[index]], self.C[coord][mutate_indexs[index+1]] = \
self.C[coord][mutate_indexs[index+1]], self.C[coord][mutate_indexs[index]]
# 开始迭代
def run(self):
cal = self.cal_level
self.best_eval = self.__get_best__()
# 保存当前染色体适应值
tmps = []
while cal > 0:
# 选择
self.__select__()
#交配
self.__mating__()
#变异
self.__mutate__()
#重新评估染色体适应值,更新Best
tmp_best_eval = self.__get_best__()
self.best_eval = tmp_best_eval if tmp_best_eval < self.best_eval else self.best_eval
# print("第{0}次迭代后,染色体适应值为:{1}, 当前最大适应值为:{2}".format(self.cal_level-cal+1, tmp_best_eval, self.best_eval))
tmps.append(self.best_eval)
cal -= 1 #迭代次数减一
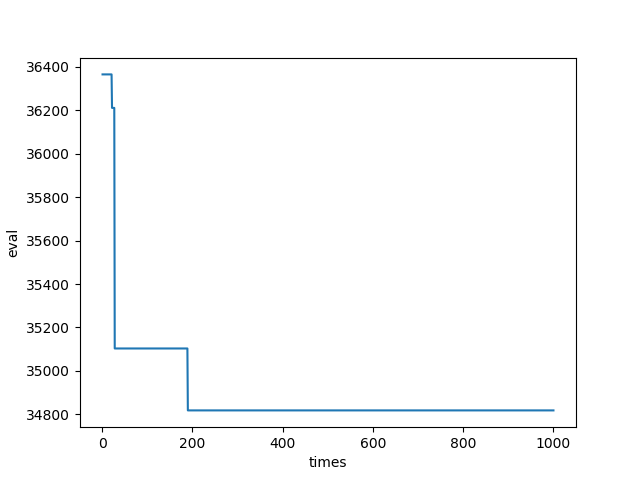
plt.plot([x for x in range(1, len(tmps)+1)], tmps)
plt.xlabel(u"times")
plt.ylabel(u"eval")
plt.show()
X = []
Y = []
for c in self.C[self.min_index]:
X.append(c[0])
Y.append(c[1])
X.append(self.C[self.min_index][0][0])
Y.append(self.C[self.min_index][0][1])
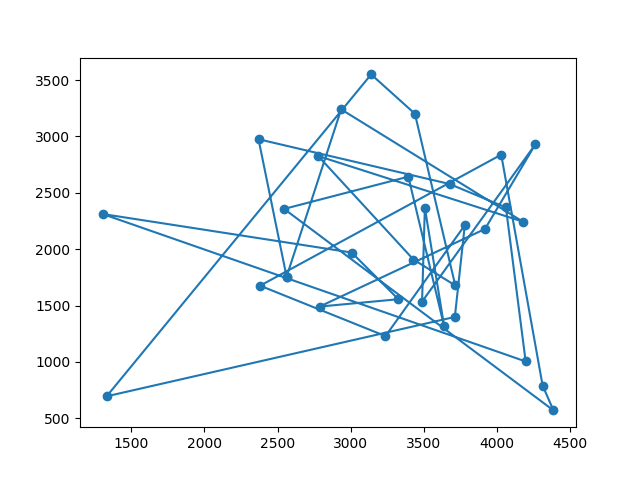
plt.plot(X, Y, 'o-')
plt.show()
return self.get_eval()
def get_eval(self):
return self.best_eval
if __name__ == "__main__":
sol = Solution()
print(sol.run())
迭代次数与适应值关系图
绘出解法中连通各城市的结果图
Comments