线段树简介

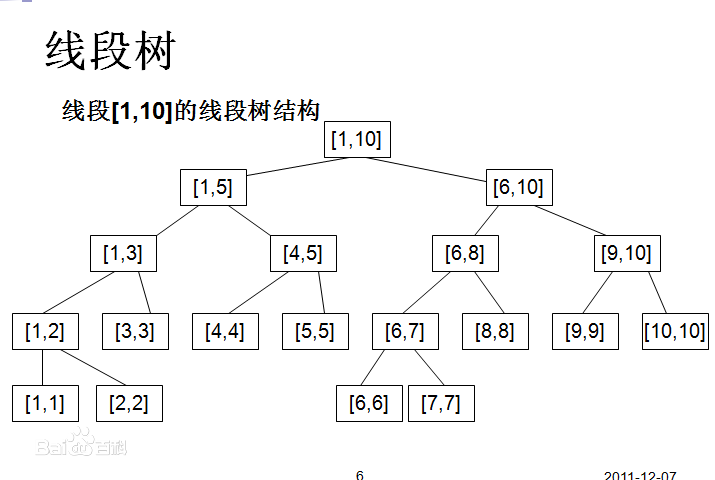
线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。

使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN）。而未优化的空间复杂度为2N，因此有时需要离散化让空间压缩。

线段树至少支持下列操作：

Insert(t,x）：将包含在区间 int 的元素 x 插入到树t中；

Delete(t,x）：从线段树 t 中删除元素 x；

Search(t,x）：返回一个指向树 t 中元素 x 的指针。

重要操作代码实现

const int N = 100006;
 struct Record{
    int l;
    int r;
    int v = 0;
 }record[N];
 
 # 建立线段树 
 void build_tree(const int k , const int l, const int r){
    record[k].l = l;
    record[k].r = r;
    if(l == r)return;
    int mid = (l+r) >> 1;
    build_tree(k << 1, l, mid);
    build_tree(k << 1 | 1, mid+1, r);
 }
 
 # 向区间插入一个点 
 void insert(const int k, const int val){
    int l = record[k].l;
    int r = record[k].r;
    if(l == r){
       record[k].v = 1;
       return;
    }
    int mid = (l+r) >> 1;
    if(val <= mid)insert(k << 1, val);
    else insert(k << 1 | 1, val);
    record[k].v = record[k << 1].v + record[k << 1 | 1].v;
 }
 
 # 删除一个点 
 void del(const int k, const int val){
    int l = record[k].l;
    int r = record[k].r;
    if(l == r){
       record[k].v = 0;
       return;
    }
    int mid = (l+r) >> 1;
    if(val <= mid)del(k << 1, val);
    else del(k << 1 | 1, val);
    record[k].v = record[k << 1].v + record[k << 1 | 1].v;
 }
 
 # 查找区间的一个点 
 int find_val(const int k, const int val){
    int l = record[k].l;
    int r = record[k].r;
    if(l == r){
       return record[k].v;
    }
    int mid = (l+r) >> 1;
    if(val <= mid)return find_val(k << 1, val);
    else return find_val(k << 1 | 1, val);
 }
 
 # 计算一个区间的点数   
 int get_sum(const int k, const int l, const int r){
    if(l == record[k].l && r == record[k].r){
       return record[k].v;
    }
    int mid = (record[k].l + record[k].r) >> 1;
    if(l > mid){
       return get_sum(k << 1 | 1, l, r);
    }else if(r <= mid){
       return get_sum(k << 1, l, r);
    }else{
       return get_sum(k << 1, l, mid) + get_sum(k << 1 | 1, mid+1, r);
    }
 }

例题，leetcode 307

Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.

The update(i, val) function modifies nums by updating the element at index i to val.

Example:

Given nums = [1, 3, 5]

sumRange(0, 2) -> 9

update(1, 2)

sumRange(0, 2) -> 8

Note:

The array is only modifiable by the update function.

You may assume the number of calls to update and sumRange function is distributed evenly.

代码求解

class NumArray {
public:
    NumArray(vector<int> nums) {
        int len = nums.size();
        m_len = len;
        if(len != 0){
            record = new Record[2*len + len/2];
            build_tree(1, 0, len-1);
            for(int i = 0; i < len; ++i){
                push_val(1, i, nums[i]);
            }
        }
       
    }
    
    void update(int i, int val) {
        push_val(1, i, val);
    }
    
    int sumRange(int i, int j) {
        return get_sum(1, i, j);
    }
    
    virtual ~NumArray(){
        delete [] record;
    }
    
private:
    
    struct Record{
        int l;
        int r;
        int val = 0;
    };
    
    int m_len = 0;
    Record * record = nullptr;
    
    void build_tree(const int k, const int l, const int r){
        record[k].l = l;
        record[k].r = r;
        if(l == r)return;
        int mid = (l+r) >> 1;
        build_tree(k << 1, l, mid);
        build_tree(k << 1 | 1, mid+1, r);
    }
    
    void push_val(const int k, const int cur, const int val){
        int l = record[k].l;
        int r = record[k].r;
        if(l == r){
            record[k].val = val;
            return;
        }
        int mid = (l+r) >> 1;
        if(cur <= mid)push_val(k << 1, cur, val);
        else push_val(k << 1 | 1, cur, val);
        record[k].val = record[k << 1].val + record[k << 1 | 1].val;
    }
    
    int get_sum(const int k, const int l, const int r){
         if(l == record[k].l && r == record[k].r){
            return record[k].val;
        }
        int mid = (record[k].l + record[k].r) >> 1;
        if(r <= mid){
            return get_sum(k << 1, l, r);
        }else if(l > mid){
            return get_sum(k << 1 | 1, l, r);
        }else{
            return get_sum(k << 1, l, mid) + get_sum(k << 1 | 1, mid+1, r);
        }
    }
    
};